Расчет изгибающего усилия при свободном изгибе листогибочного станка

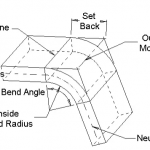
В последние годы станки для гибки металла с тормозом широко используются в различных отраслях промышленности, и спектр обработки гибочных станков расширяется. Однако систематического обсуждения расчета изгибающей силы не проводилось. В настоящее время существует примерно два типа формул расчета силы изгиба, рекомендуемых в руководствах различных производителей листогибочных машин.

Р - изгибающее усилие, кН;

S - толщина листа, мм;

l - длина изгиба листа, м;

V - ширина нижнего отверстия матрицы, мм;

σb - предел прочности материала при растяжении, МПа.

Таблица параметров силы изгиба, рекомендуемая производителем, также рассчитывается по приведенной выше формуле.

Процесс вывода и область применения формулы расчета силы изгиба

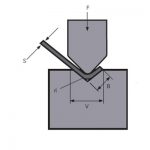
На рис. 1 представлена схема работы при гибке листа. Ниже описывается процесс получения формулы расчета изгибающей силы и два дополнительных параметра. Во-первых, такие рекомендации есть в инструкции к товару. При свободной гибке выбранная ширина нижнего отверстия матрицы V в 8-10 раз превышает толщину листа S. Здесь мы принимаем соотношение сторон .

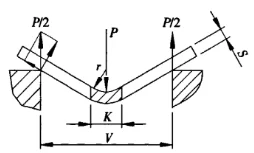
Рисунок 1 Принципиальная схема гибки

P - изгибающая сила

S - толщина листа

V - ширина раскрытия нижней матрицы

r - внутренний радиус при изгибе листа

K - ширина горизонтальной проекции зоны деформации изгиба=9

Во-вторых, производитель указывает соответствующие значения ширины матрицы V и внутреннего диаметра r изгибаемой заготовки в таблице параметров силы изгиба. Обычно r=(0,16~0,17)В. Здесь отношение диаметра к ширине =0.16.

В процессе гибки листового металла материал в очаге деформации находится в состоянии высокопластической деформации и изгибается под углом вокруг осевой линии. На внешней поверхности зоны изгиба в некоторых случаях могут появляться микротрещины. На сечении очага деформации, кроме окрестности центрального слоя, напряжения в остальных точках близки к пределу прочности материала. Верхняя часть нейтрального слоя сжата, а нижняя натянута. На рис. 2 представлены поперечное сечение и соответствующая диаграмма напряжений в очаге деформации.

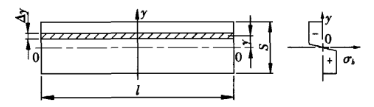
Рисунок 2 Диаграмма напряжений

S - толщина листа

l - длина изгиба листа

Изгибающий момент на поперечном сечении очага деформации равен:

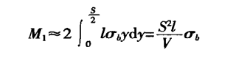
Изгибающий момент, создаваемый изгибающей силой машины в очаге деформации, составляет (см. рис. 1):

От

При использовании пресс-форм общего назначения для свободной гибки на гибочном станке большая часть листового металла изгибается под углом 90°. Как показано на рисунке 3. K равно:

Подставляя K в уравнение (1), получаем:

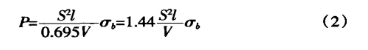
Предел прочности обычных материалов σb=450 Н/мм2, подставляя формулу (2) в:

Из процесса вывода видно, что при использовании уравнения (2) или уравнения (3) для расчета изгибающей силы два дополнительных

должны быть соблюдены условия параметров, упомянутые выше. То есть соотношение сторон=9, отношение диаметра к ширине=0,16, иначе будет большая ошибка.

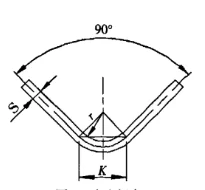
Рисунок 3 Свободный изгиб

S - толщина листа

r - внутренний радиус при изгибе листа

K - ширина горизонтальной проекции зоны деформации изгиба

Новые методы и этапы расчета силы изгиба

Из-за требований к конструкции или процессу иногда бывает трудно одновременно выполнить два вышеуказанных дополнительных требования. В настоящее время рекомендуемая формула расчета не должна использоваться для расчета силы изгиба, а должна выполняться в соответствии со следующими шагами.

(1) В соответствии с толщиной листа S, радиусом изгиба r и нижним отверстием матрицы V соответственно рассчитываются отношение ширины к толщине и отношение диаметра к ширине.

(2) Рассчитайте ширину проекции зоны деформации в соответствии с деформацией листа.

(3) Примените формулу (1) для расчета изгибающей силы.

В процессе расчета учитывалась разница радиуса изгиба и изменение соответствующей зоны деформации. Изгибающее усилие, рассчитанное из этого, является более точным и надежным, чем результат, рассчитанный по обычно рекомендуемой формуле. Теперь приведите пример для иллюстрации, как показано на рисунке 4.

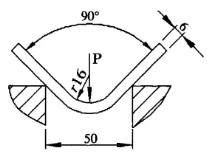
Рисунок 4 Новый метод расчета

Известны: Толщина листа S=6мм, длина листа l=4м, радиус изгиба r=16мм, ширина нижнего отверстия матрицы V=50мм, предел прочности материала на растяжение σb=450Н/мм2. Найдите изгибающую силу, необходимую для свободного изгиба.

Во-первых, найдите соотношение сторон и отношение диаметра к ширине:

Во-вторых, вычислить ширину проекции очага деформации:

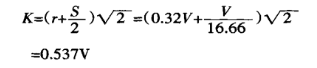
Наконец, используйте уравнение (1), чтобы найти изгибающую силу:

Если для расчета силы изгиба используется обычная рекомендуемая формула:

От = 1,5, видно, что разница между ними составляет 1,5 раза. Причина этой ошибки в том, что радиус изгиба в этом примере относительно велик, а соответствующая площадь деформации увеличена, поэтому при изгибе требуется большее изгибающее усилие. В этом примере отношение диаметра к ширине = 0,32, что превышает дополнительные условия параметров, введенные выше. Использовать обычно рекомендуемую формулу для расчета изгибающей силы явно нецелесообразно. Преимущества нового метода расчета вы можете увидеть на этом примере.

Вывод

Приведенные здесь этапы и формулы расчета изгибающего усилия применимы не только к угловому изгибу листового металла, но и к дуговому изгибу (строго говоря, его следует называть угловым изгибом с особо большим радиусом изгиба). Следует отметить, что форма формы особенная, когда лист изогнут в форме дуги. При расчете проекции очага деформации ее необходимо рассчитывать по заданным в технологическом процессе технологическим параметрам, которые не могут быть выражены простой формулой.

При проектировании дугообразной формы с использованием представленного в этой статье метода расчета изгибающей силы можно получить удовлетворительные результаты.